|
House Advantage control
BY: Mike From Hawaii
It has taken a long trip to get to a bottom line with Dice Control. First we had to determine if such a thing could exist. Could it have a physical basis in a learnable skill? We found a promising mechanism in axial control, and a more remote possibility in facial control.
Once a mechanism was available, we could create a spreadsheet that would calculate how that assumed level of control would affect the percentage appearances of the 36 possible dice rolls. From there we had to calculate the affect on the 11 numbers that drive the game of Craps. We even reasoned out how to go from a statement of "I can control the dice one out of X rolls" to facial percentages that would need to be used to simulate that level of dice control.
This finally gives interesting tables and pretty charts showing that indeed the six basic axial control dice sets do indeed change the distribution of numbers in a potentially significant way with levels of dice control that while difficult, are not super human. We had to consider all the physical constraints that construction of each die demanded. And be clear that we cannot "rob Peter" unless we "pay Paul". We must end up with certain totals right at 100%. If control enhances percentages in one area, it must suppress percentages somewhere else to restore balance.
Finally we came up with a model to convert from assumed dice control to a bottom line. All shooters are random rollers. No one can call with absolute certainty the next roll of the dice. Therefore all participants in a game of Craps will see their results, their winnings and loses vs. sequential rolls as a random walk. A random walk around a baseline.
Since the house has designed the game of Craps to have a house advantage, that is be less than a zero sum, fair bet game, the baseline will slope downwards at the house advantage loss rate. How steep your personal baseline is will depend on what bets you make since in Craps you are faced with some of the lowest and some of the highest house advantages in the casino, all mixed together on the felt. In other words, on the composite house advantage of your betting strategy.
Where true dice control comes in, is its ability to potentially alter the house advantage on specific bets. Any dice control that moves the distribution of the 36 outcomes from flat, all equal at about 2.78% each, will cause the house advantage on all Craps bets to potentially change. Some actually can remain virtually unchanged. Others will be quite sensitive to change.
Here we have a bottom line that we can examine. Finally we have slashed our way through the mathematical undergrowth of the jungle far enough to create a trail from an assumed level of dice control to a "show me the money" type of answer.
The Hardways Set
Let's look at actual numbers for a classic 1-6 1-6 axial, symmetrical set called the "Hardways Set". It is so called because when ready to throw, the top, bottom, front and back face pairs all make "hardways". Specifically, 2-2, 3-3, 4-4, and 5-5. The hard four, hard six, hard eight and hard ten.

What would this set actually accomplish if one could throw it with high quality dice control? Exactly how would you have to change your betting strategy to compensate for the affect such control would have on the 36 rolls? How would that control percolate down to the bottom line, advantageous changes in the house advantages on various bets, and disadvantageous changes in house advantage on various bets?
This is very critical information! Without it, you are far better off working hard to NOT control the dice, but have them behave in a totally random fashion. Why? When you start messing with the 36 possible results of a throw of the dice, when you move those percentages off a flat line of 2.78% each, you are going to change everything, somehow. Many bets will potentially become considerably worse for the player. If you do not know exactly which ones, you are in big trouble.
At least for the true random roller, the house advantages are well known and easy to calculate. Any betting strategy will have a composite house advantage that is knowable.
You start actually achieving some level of dice control, you give up this information and absolutely MUST get it back.
So let's look. This set is very well named. We will assume a level of control of one roll in 12. We will assume you can get it to work one out of every 12 tries. This is perhaps possible with a lot of practice, study and coaching. By selecting such a high level of control, we can get a clearer picture of where a given dice set is headed. Which house advantages it is targeting in a positive and negative direction.
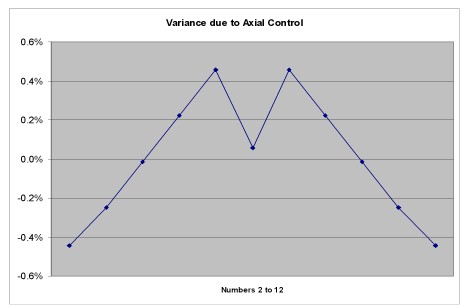
Set up for just axial control, suppressing to some extent (about 8.33%) the appearances of the ones and sixes we set on the horizontal side-to-side axis, we discover little effect on the Sevens. Sevens is our heaviest number, it has the greatest mass. It is the hardest number to control. We do see a nice effect on the lighter numbers, especially the Twos and 12's. Why? well if either die is controlled and its One does not appear, then there is zero ways to make the sum Two. If either dice is controlled so its Six does not appear, then there are zero ways to make the sum 12.
Notice that what we take away from these numbers, we get back in the summed point numbers Six and Eight. Let's look at the table:
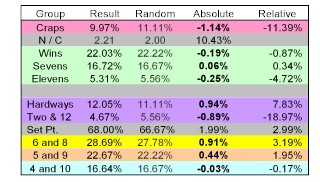
Notice that the biggest hit is focused in two places. First Craps. This makes sense. This set really targets the light numbers Two and 12. It also beats up on the four ways to make Three and 11. As a result, Craps catches the brunt of any control applied to this particular dice set.
True to its name, this set also targets the hardways, causing them to appear more often than they should. Hardways have "low mass". Only one of the 36 possible results of rolling two dice makes each of the hardways. You mess with the frequency of the face on a given die that contributes to a specific hardway, and you mess with the frequency of the that hardway in a rather focused manner.
What we end up with is a dice set that on the come out roll will suppress immediate losses due to Craps. It will have an increased chance of setting a point. When it does set a point it will tend to set Six and Eight more than other points. It also slightly favors the Five and Nine as points. Since it does not like 11's, its affect on wins due to Naturals on the come out roll will be diluted, actually negative.
What about the bottom line? The affect on house advantages? What about specific bets on the felt?
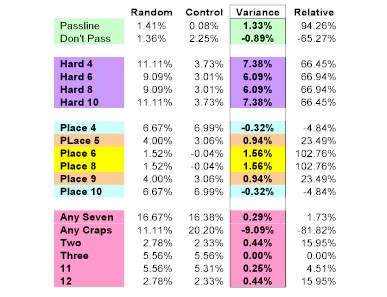
Well since it also increases the chances of setting and then making a point, especially Sixes and Eights, the house advantage on a pass line bet is down from 1.41% to close to zero, just 0.08%. Since it thumps on Craps and Craps is the wrong better's friend, you can see that Don't Pass would not be a good bet with this set if control is actually working. House advantage on that bet soars to 2.25%.
Take a hard look at the Place Six and Place Eight bet. They actually go negative by a tiny amount. That means if this were actually working as advertised, the baseline on these bets would be better than square, they would slightly be in favor of the shooter, and of course all of his friends along for the ride.
The Hard Six and the Hard Eight have really be smacked around. Unfortunately those bets start with a whopping 9.09% house advantage. Slicing that to 3% is impressive, but that is still a lot of house advantage.
What about Seven, people are always going on about Sevens. Well betting Big Red is of course donating your money to the "Casino Management Relief Fund", a non-tax deductible donation. But it does provide a measure focused on Sevens. It slides a bit in your favor, by a relative 1.73%. But it is still at a whopping "stick'um up" 16.38%. And due to the suppression of Craps, the any Craps bet has taken the lead as the worst bet in the entire Casino! It is now in their favor by 20.20%, having beaten out Big Red for that dubious honor.
As bar graphs it looks like this:
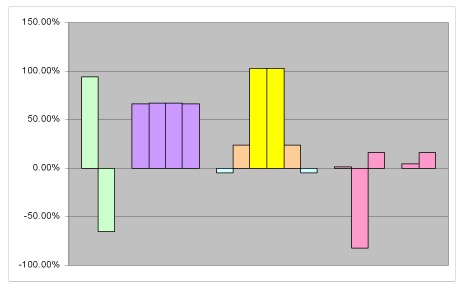
Here we have graphed the exaggerated variations of the affect of this level of assumed axial dice control with the Hardways Set. The two green lines are pass line and don't pass. The purples are the four hardways, the light blues are the Place Four and Ten, the oranges the Place Five and Nine and the yellows are the Place Six and Eight. The reds are the selected prop bets with the big one heading downwards into your pocket being the Any Craps bet.
So finally, bottom line. If you put in the practice, if you had the professional coaching, if you had dice control, you could mess with the distribution of the percentage appearances of the 36 possible outcomes of a roll of two dice. It takes several steps, permutations if you will, to go from such an assumption to the affect on the house advantages such control might offer.
It is critically important to know exactly where all this is headed because some bets are going to get better for the player/shooter, and some bets are going to get worse. If you do not adapt your betting strategy exactly right, you could work hard, practice a lot and get much better at shooting yourself in the foot.
Click Here to return to the list of prior articles ...
|
 |















